Dziś geometria ;P

W pracy ostatnio pojawił się problem – czy wierzchołki wielokąta są ułożone zgodnie z kierunkiem ruchu wskazówek zegara czy wręcz przeciwnie? Potrzebna była szybka i tania (w sensie obliczeniowym) metoda określenia owego ułożenia.

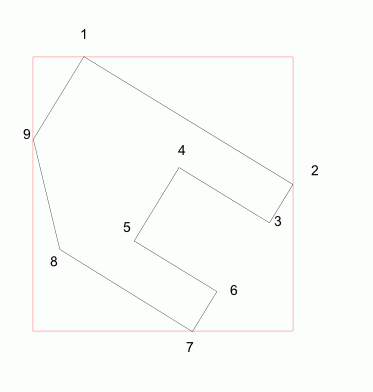
Ok, patrząc na obrazek widzimy od razu ;P A programowo?

Jak widać na rysunku wyznaczamy sobie 4 (w pewnych szczególnych przypadkach 3) punkty brzegowe – górny, prawy, dolny, lewy – opisując prostokąt na wielokącie. Znalezienie tych punktów jest proste i tanie – wystarczy raz przejrzeć listę współrzędnych.

Zapisujemy sobie numery tych punktów prawoskrętnie do array-a: 1,2,7,9. Jeśli ciąg jest rosnący – mamy prawoskrętny. Jeśli malejący – lewoskrętny.

Ok, a co, jeśli nam się figura obróci o 180 stopni i dostaniemy: 7,9,1,2 ? Ciąg nie jest już rosnący ;P Rozwiązań jest parę. Można szukać punktu nieciągłości i próbować splice tablicy zrobić i merge potem. Można sprawdzić, jaki jest największy element w tablicy i dodać taką wartość do wszystkich mniejszych. Przy 4 elementach będzie to nadal szybkie i proste: 7, 9, 10(1+9), 11(2+9).

Jak sprawdzić, czy ciąg jest rosnący?

$up = $points;
sort($up);
if(join($up)==join($points))
{
echo "rosnący";
}


Cała operacja jest prosta i szybka – zależna liniowo od ilości wierzchołków wielokąta.